Zasady oceniania
Sposób weryfikacji poprawności rozwiązania zależy od typu
zadania. Poniżej przedstawione są tego ogólne zasady. Jeśli chcesz
zobaczyć, jak sprawdzono konkretne zadanie, przejdź do opisu oceniania
zawartego w dziale, z którego pochodzi zadanie.
Spis treści
Podstawowe
Za rozwiązania niektórych zadań można otrzymać
tylko zero lub maksymalną liczbę punktów.
Za
dobre rozwiązanie otrzymasz maksymalną liczbę punktów,
tzn. 100% punktów (najczęściej jest to 10
punktów), za rozwiązanie błędne 0
punktów.
Każdy błąd, nawet niewielki, skutkuje obniżeniem oceny do zera.
Taki sposób oceniania stosowany jest w przypadku
prostych
zadań, których rozwiązanie polega np. na podaniu jednej
liczby.
Jest to
sposób
oceniania na zasadzie 0 lub 100%
przystosowany do zadań, w których musisz podać więcej
niż jedną liczbę. Gdy rozwiązanie zadania polega na podaniu n liczb, to otrzymasz 100%
: n punktów za każdą
poprawnie wpisaną liczbę.
Przykład
rozwiązania:
Jeśli poprawne rozwiązanie składa się z dwóch
liczb, to otrzymasz 50% punktów za każdą poprawnie
wpisaną liczbę. Jeśli rozwiązanie wymaga wpisania trzech liczb,
to otrzymasz 33% punktów za każdą poprawnie wpisaną liczbę.
Jeśli w rozwiązaniu muszą być cztery
liczby, otrzymasz 25% punktów za każdą poprawnie wpisaną
liczbę itd.
Gdy rozwiążesz zadanie poprawnie, lecz przy zapisie
popełnisz błąd (nazywany drobnym błędem), utracisz część
punktów przysługujących za poprawne rozwiązanie. W
większości zadań drobne błędy powodują stratę 20% punktów.
Rodzaje drobnych błędów:
-
Nadmiarowe
zera — np. poprawne rozwiązanie to
liczba 1,
a wprowadziłeś liczbę 1,0.
-
Zbędny przecinek — np.
poprawne rozwiązanie to
liczba 1,
a wpisałeś przecinek po liczbie: 1,.
-
Liczba całkowita zapisana jako
ułamek — np.
poprawne rozwiązanie to liczba 1,
a wprowadziłeś liczbę 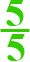 .
.
-
Błędny zapis — np. poprawne
rozwiązanie to liczba 1,2,
a wprowadziłeś 1,,2.
-
Ułamek skracalny — np. poprawne
rozwiązanie to liczba 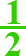 ,
a wprowadziłeś liczbę
,
a wprowadziłeś liczbę 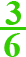 .
.
-
Błędne wybrana liczba mieszana — wybrałeś
formatkę  zamiast
zamiast  , np. poprawne
rozwiązanie to ułamek
, np. poprawne
rozwiązanie to ułamek 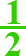 ,
a wprowadziłeś liczbę mieszaną 0
,
a wprowadziłeś liczbę mieszaną 0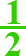 .
.
-
Pozostawienie niewymierności w mianowniku.
Przykład
rozwiązania: Jeśli prawidłowe rozwiązanie to
liczby  oraz 2,
a wpisałeś rozwiązanie
oraz 2,
a wpisałeś rozwiązanie  oraz
2,
to nie otrzymasz pełnej liczby punktów. W rozwiązaniu
podałeś
poprawne liczby, jednak jednej z nich nie skróciłeś.
Otrzymasz wówczas maksymalną liczbę punktów za
wpisanie 2
(50%), a za wpisanie liczby
oraz
2,
to nie otrzymasz pełnej liczby punktów. W rozwiązaniu
podałeś
poprawne liczby, jednak jednej z nich nie skróciłeś.
Otrzymasz wówczas maksymalną liczbę punktów za
wpisanie 2
(50%), a za wpisanie liczby  otrzymasz
tylko
80% dostępnych punktów: 80% z 50% wynosi 40%. W sumie otrzymasz 90% punktów.
otrzymasz
tylko
80% dostępnych punktów: 80% z 50% wynosi 40%. W sumie otrzymasz 90% punktów.
Wzory
Niektóre rozwiązania oceniane są według
skomplikowanego wzoru.
Metodę tę stosuje się wtedy, gdy w
rozwiązaniu musisz podać kilka liczb, np. znaleźć miejsca
zerowe funkcji lub wypisać
wartości najmniejsze i największe funkcji. Przy ocenieniu takich zadań
stosuje się wzór:
100% · liczba
elementów(R∩U) : liczba
elementów(R∪U),
gdzie R jest zbiorem zawierającym prawidłowe rozwiązanie,
natomiast U jest zbiorem składającym się z Twojego rozwiązania. Znak ∩
oznacza część wspólną
(przekrój) zbiorów, a ∪ jest
sumą zbiorów.
Przykład
rozwiązania: Jeśli prawidłowym rozwiązaniem zadania są
liczby
–1,
1
oraz 5,
to
R={–1; 1; 5}. Jeśli wpisałeś rozwiązanie 1 oraz
5,
to
U={1; 5}.
Wówczas R∩U={1; 5},
a R∪U={–1; 1; 5}.
Ocena, którą uzyskasz to 100% · 2 :
3 = 67% punktów.
Przykład
rozwiązania: Jeśli prawidłowym rozwiązaniem zadania są
liczby
0,
2
oraz 4,
to
R={0; 2; 4}. Jeśli wpisałeś rozwiązanie 1,
3
oraz 5,
to
U={1; 3; 5}.
Wówczas R∩U=∅ (zbiór
pusty),
a R∪U={0; 1; 2; 3; 4; 5}.
Ocena, którą uzyskasz to 100% · 0 :
6 = 0 punktów.
Przykład
rozwiązania: Jeśli prawidłowym rozwiązaniem zadania są
liczby
1,
2
oraz
3, to
R={1; 2; 3}. Jeśli wpisałeś rozwiązanie
1,
2 oraz
4, to
U={1; 2; 4}.
Wówczas R∩U={1; 2},
a R∪U={1; 2; 3; 4}.
Ocena, którą uzyskasz to 100% · 2 :
4 = 50% punktów.
Jest to uogólnienie metody Ocenianie
liczb. Zasady są
takie same, lecz zamiast liczb program bierze pod uwagę bardziej
skomplikowane obiekty: przedziały lub wykreślone części funkcji.
Wzór wyznaczający ocenę pozostaje ten sam:
100% · liczba
elementów(R∩U) : liczba
elementów(R∪U),
gdzie R jest zbiorem, którego elementy tworzą
prawidłowe rozwiązanie,
natomiast U jest zbiorem składającym się z Twojego rozwiązania. Znak ∩
oznacza część wspólną
(przekrój) zbiorów, a ∪ jest
sumą zbiorów.
Przykład
rozwiązania: Jeśli prawidłowym rozwiązaniem zadania są
przedziały [0; 1]
oraz (2;
5],
to
R={[0; 1]; (2; 5]}. Jeśli wpisałeś rozwiązanie [0; 1],
to
U={[0; 1]}.
Wówczas R∩U={[0; 1]},
a R∪U={[0; 1]; (2; 5]}.
Ocena, którą uzyskasz to 100% · 1 :
2 = 50% punktów.
Przykład
rozwiązania: Jeśli prawidłowym rozwiązaniem zadania są
przedziały [0; 1]
oraz (2;
5],
to
R={[0; 1]; (2; 5]}. Jeśli wpisałeś rozwiązanie [0; 1]
oraz (2;
5), to
U={[0; 1]; (2; 5)}.
Wówczas R∩U={[0; 1]},
a R∪U={[0; 1]; (2; 5]; (2; 5)}.
Ocena, którą uzyskasz to 100% · 1 :
3 = 33% punktów.
Przykład
rozwiązania: W przypadku zadań, w których musisz
narysować wykres funkcji, program porównuje elementy
wykresu poprawnego rozwiązania i Twojego rozwiązania.
| R, czyli prawidłowe
rozwiązanie składa
się z 5
elementów i wygląda tak: |
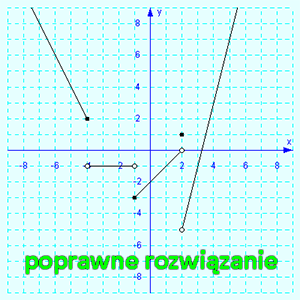 |
|
U, czyli Twoje
rozwiązanie także składa się z 5 elementów
i wygląda następująco: |
 |
| |
|
|
|
|
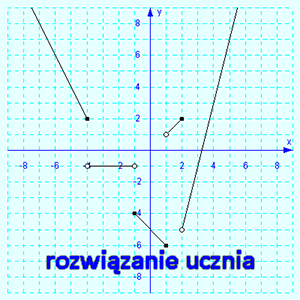
Część
wspólna (przekrój R∩U) rozwiązania
poprawnego
i Twojego rozwiązania.
3 elementy: |
 |
|
Suma R∪U elementów składających się
na rozwiązanie
prawidłowe
i Twoje rozwiązanie (nie jest to już wykres funkcji!).
7
elementów: |
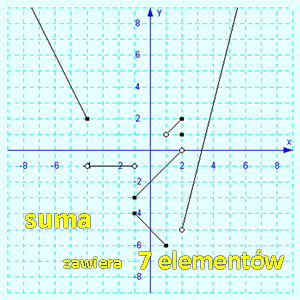 |
Zatem
za takie rozwiązanie otrzymasz 100% · 3 : 7 = 43%
punktów.
Ocenianie
kolejności
W niektórych zadaniach należy uporządkować liczby w kolejności
rosnącej lub malejącej. Rozwiązanie takich zadań program ocenia w
następujący sposób: Bierze pod uwagę wszystkie pary liczb
występujące w
zadaniu i sprawdza, czy dana para jest ustawiona w kolejności wymaganej
w treści zadania. Jeśli przynajmniej połowa par jest ustawiona w dobrej
kolejności, to ocena za to zadanie jest równa
liczbie par
ustawionych w dobrej kolejności podzielonej przez liczbę wszystkich
par. W przeciwnym przypadku ocena wynosi zero.
Na
przykład: W zadaniu o treści: Uporządkuj rosnąco liczby 4;
–0,7; 2,5;
–2,5 musisz
ustawić cztery liczby w kolejności
rosnącej, a więc zapełnić cztery miejsca:
| miejsce nr 1 |
miejsce nr 2 |
miejsce nr 3 |
miejsce nr 4 |
Przypuśćmy, że ustawisz liczby w następującej
kolejności:
| –0,7
|
2,5
|
–2,5
|
4 |
| miejsce nr 1 |
miejsce nr 2 |
miejsce nr 3 |
miejsce nr 4 |
Program porównuje pary liczb występujące w
rozwiązaniu:
-
para liczb stojących na miejscu nr 1 i miejscu
nr 2: –0,7
i 2,5,
-
para liczb stojących na miejscu nr 1 i miejscu
nr 3: –0,7
i –2,5,
-
para liczb stojących na miejscu nr 1 i miejscu
nr 4: –0,7
i 4,
-
para liczb stojących na miejscu nr 2 i miejscu
nr 3: 2,5
i –2,5,
-
para liczb stojących na miejscu nr 2 i miejscu
nr 4: 2,5
i 4,
-
para liczb stojących na miejscu nr 3 i miejscu
nr 4: –2,5
i 4.
Następnie program sprawdza, które z tych par są
poprawnie
uporządkowane, tzn. liczby są w kolejności rosnącej.
Są to cztery
pary: A, C, E oraz F. W zadaniu występuje sześć par, więc
więcej niż połowa par jest poprawna. Zatem za
takie rozwiązanie zadania otrzymasz:
4 : 6
· 100% = 67% punktów.
Ocenianie
wielomianów
Jeśli w rozwiązaniu zadania należy wpisać wielomian, program
oceni takie rozwiązanie w następujący sposób. Najpierw program oblicza
parametr:
stmax
= (większy ze stopni: stopień wielomianu w prawidłowym rozwiązaniu i
stopień wielomianu w Twoim rozwiązaniu) + 1.
Na
przykład: Jeśli prawidłowe rozwiązanie to wielomian x4
+ 2
x2 –
5, a w Twoim rozwiązaniu będzie x3
+ 2
x2
+
5, to stmax = 4 + 1 = 5.
Na
przykład: Jeśli prawidłowe rozwiązanie to wielomian 2 x2 –
1, a w Twoim rozwiązaniu będzie x3
+ 2
x2 –
1, to stmax = 3 + 1 = 4.
Następnie program liczy, ile ze współczynników
wielomianu, którego wpisałeś w
rozwiązaniu jest nieprawidłowych:
w = liczba nieprawidłowych
współczynników w rozwiązaniu.
Na
przykład: Jeśli prawidłowe rozwiązanie to wielomian x3
+ 2
x –
5, a
wpiszesz w rozwiązaniu x3
+ 2
x + 5,
to jeden współczynnik jest nieprawidłowy, czyli w = 1:
| stopień |
współczynniki
prawidłowe |
współczynniki
ucznia |
| 3 |
1 |
1 |
| 2 |
0 |
0 |
| 1 |
2 |
2 |
| 0 |
– 5 |
5 |
Na
przykład: Jeśli prawidłowe rozwiązanie to wielomian 5 x4
+ 2
x2 – x –
2, a
wpiszesz w rozwiązaniu 5 x3
+ 2
x2 – x +
2,
to trzy współczynniki są nieprawidłowe, czyli w = 3:
| stopień |
współczynniki
prawidłowe |
współczynniki
ucznia |
| 4 |
5 |
0 |
| 3 |
0 |
5 |
| 2 |
2 |
2 |
| 1 |
– 1 |
– 1 |
| 0 |
– 2 |
2 |
Przy ocenianiu, program bierze pod uwagę następujące błędy:
-
r — redukcja wielomianu: jeśli wielomian nie jest
zredukowany, to r = 1; jeśli jest r = 0,
-
u — uporządkowanie wielomianu: jeśli
wielomian nie jest uporządkowany, to u = 1; jeśli jest u = 0.
Ostateczna ocena będzie równa:
100% – 100%
· 2 · w : stmax –
20% · (r + u).
Przykład
rozwiązania: Jeśli prawidłowe rozwiązanie to wielomian x4
+ x2 –
2 x
, a wpiszesz x3
+ x2 –
2 x
, to ocena będzie wyglądała następująco.
Parametr stmax
= 4 + 1 = 5. Porównanie współczynników wielomianu:
| stopień |
współczynniki
prawidłowe |
współczynniki
ucznia |
| 4 |
1 |
0 |
| 3 |
0 |
1 |
| 2 |
1 |
1 |
| 1 |
– 2 |
– 2 |
| 0 |
0 |
0 |
Widać, że dwa współczynniki są nieprawidłowe, więc w = 2.
Wielomian w rozwiązaniu jest zredukowany i uporządkowany, a zatem r = u
= 0. Ostateczna ocena to:
100% – 100%
· 2 · w : stmax –
20% · (r + u) = 100% – 100% · 2 · 2
: 5 – 20% · (0 + 0)
= 100% – 100%
· 4 : 5 – 20% · 0 =
= 100% –
80% – 0 = 20%.
Przykład
rozwiązania: Jeśli prawidłowe rozwiązanie to wielomian 5 x3
– 11 x2 –
2 x
+ 3
, a wpiszesz x2
+ 5 x3 –
12 x2
+ 3 – 2 x
, to ocenianie będzie przebiegało następująco:
Widać, że podany wielomian nie jest zredukowany, ponieważ
we wpisanym rozwiązaniu dwa razy występuje potęga x2.
Ponadto wielomian nie jest uporządkowany, gdyż potęgi zmiennej x nie
są ułożone od największej do najmniejszej. Zatem współczynniki r oraz u
będą miały wartość 1. Po zredukowaniu i uporządkowaniu wielomianu
okazuje się, że wielomian w Twoim rozwiązaniu ma poprawne współczynniki
(w = 0). Ocena to:
100% – 100%
· 2 · w : stmax –
20% · (r + u) = 100% – 100% · 2 · 0
: 5 – 20% · (1 + 1)
= 100% – 100% · 0 – 20% ·
2 =
= 100% – 0 –
40% = 60%.
Program stosuje także następującą metodę oceniania wielomianów.
Jeśli
wpiszesz w rozwiązaniu wielomian, który jest różny co do
wartości od wielomianu w prawidłowym rozwiązaniu, otrzymujesz 0
punktów.
Na
przykład: Jeśli prawidłowe rozwiązanie to wielomian x4
+ 2
x2 –
5, a w Twoim rozwiązaniu będzie x3
+ 2
x2
+
5, to nie dostaniesz żadnych punktów za to rozwiązanie.
Na
przykład: Jeśli prawidłowe rozwiązanie to wielomian 2 x2 –
1, a w Twoim rozwiązaniu będzie 2
x2 – x – 1 + x, to
te dwa wielomiany mają takie same wartości, choć program odejmie kilka
punktów za brak redukcji i nieuporządkowanie wielomianu.
Przy ocenianiu program bierze jeszcze pod uwagę następujące
błędy:
-
s — niepoprawny stopień wielomianu (stopień za duży lub
za mały),
-
r — wielomian niezredukowany,
-
u — wielomian nieuporządkowany,
-
b — drobny błąd.
Uwaga!
Wszystkie powyżej wymienione parametry przyjmują wartość 1 — gdy
opisany błąd występuje w rozwiązaniu lub 0 — gdy nie
popełniłeś danego błędu wpisując wielomian.
Jeśli wpisałeś w rozwiązaniu prawidłowy
wielomian, ale jego postać nie jest idealna, to
Twoja ocena będzie liczona według wzoru:
100% – 50%
· s –
20% · (r + u + b).
Przykład
rozwiązania: Przypomnijmy poprzedni przykład: prawidłowe
rozwiązanie to wielomian 2 x2 –
1, a w Twoim rozwiązaniu jest 2
x2 – x – 1 + x.
Wielomian, który napisałeś ma te same wartości, co prawidłowa
odpowiedź, ale jest niezredukowany i nieuporządkowany, a zatem
parametry r oraz u przyjmą wartość 1. Ostateczna ocena to:
100% – 50%
· s –
20% · (r + u + b) = 100% – 50%
· 0 –
20% · (1 + 1 + 0) = 100% – 0 –
20% · 2 = 100% – 40% = 60%.
Przykład
rozwiązania: Jeśli prawidłowe rozwiązanie to wielomian 5 x3
– 11 x2 –
2 x
+ 3
, a wpiszesz x4
– x4
+ 5 x3 –
11 x2
– 2 x
+ 3, to wpisany wielomian ma prawidłowe wartości,
ale jego stopień jest za duży i wielomian jest niezredukowany, zatem s
= r = 1. Otrzymasz następującą ocenę:
100% – 50%
· s –
20% · (r + u + b) = 100% – 50%
· 1 –
20% · (1 + 0 + 0) = 100% – 50% –
20% · 1 = 100% – 70% = 30%.
Tutaj wielomian wpisany w rozwiązaniu oceniany jest sposobem
mieszanym — część zasad pochodzi z Oceniania wielomianów I,
część z Oceniania
wielomianów II. Podajemy tutaj tylko odpowiednie wzory użyte
przy ocenianiu. Jeśli chcesz znaleźć dokładny opis i przykłady
oceniania, zajrzyj do dwóch pierwszych opisów oceniania wielomianów: Ocenianie wielomianów I
i Ocenianie wielomianów
II.
Najpierw program oblicza
parametr:
stmax
= (większy ze stopni: stopień wielomianu w prawidłowym rozwiązaniu i
stopień wielomianu w Twoim rozwiązaniu) + 1.
Następnie program liczy, ile ze współczynników
wielomianu, które wpisałeś w
rozwiązaniu jest nieprawidłowych:
w = liczba nieprawidłowych
współczynników w rozwiązaniu.
Przy ocenianiu program bierze pod uwagę następujące błędy:
-
s — niepoprawny stopień wielomianu (stopień za duży lub
za mały),
-
r — wielomian niezredukowany,
-
u — wielomian nieuporządkowany,
-
b — drobny błąd.
Uwaga!
Wszystkie powyżej wymienione parametry przyjmują wartość 1 — gdy
opisany błąd występuje w rozwiązaniu lub 0 — gdy nie
popełniłeś danego błędu wpisując wielomian.
Ostateczna ocena będzie liczona ze wzoru:
100% – 100%
· w : stmax – 50% · s
–
5% · (r + u) –
2% · b.
Wielomian wpisany w rozwiązaniu oceniany jest sposobem
mieszanym — część zasad pochodzi z Oceniania
wielomianów I,
część z Oceniania
wielomianów II. Istotną różnicą pomiędzy tym
sposobem oceniania, a sposobami oceniania wielomianów opisanymi powyżej
jest natychmiastowe obniżenie oceny do zera, jeśli wielomian we
wpisanym rozwiązaniu ma za duży stopień.
Podajemy tutaj tylko odpowiednie wzory użyte
przy ocenianiu. Jeśli chcesz znaleźć dokładny opis i przykłady
oceniania, zajrzyj do dwóch pierwszych opisów oceniania wielomianów: Ocenianie
wielomianów I
i Ocenianie
wielomianów
II.
Najpierw program oblicza
parametr:
stmax
= (większy ze stopni: stopień wielomianu w prawidłowym rozwiązaniu i
stopień wielomianu w Twoim rozwiązaniu) + 1.
Następnie program liczy, ile ze współczynników
wielomianu, które wpisałeś w
rozwiązaniu jest nieprawidłowych:
w = liczba nieprawidłowych
współczynników w rozwiązaniu.
Przy ocenianiu program bierze pod uwagę następujące błędy:
-
z — stopień wielomianu jest za duży (większy
niż stopień wielomianu w prawidłowej odpowiedzi),
-
r — wielomian niezredukowany,
-
u — wielomian nieuporządkowany,
-
b — drobny
błąd.
Uwaga!
Wszystkie powyżej wymienione parametry przyjmują wartość 1 — gdy
opisany błąd występuje w rozwiązaniu lub 0 — gdy nie
popełniłeś danego błędu wpisując wielomian.
Ostateczna ocena będzie liczona ze wzoru:
100% – 100%
· w : stmax – 100% ·
z –
5% · (r + u) –
2% · b.
Wielomian wpisany w rozwiązaniu oceniany jest sposobem
mieszanym — część zasad pochodzi z Oceniania
wielomianów I,
część z Oceniania
wielomianów II. Istotną różnicą pomiędzy tym
sposobem oceniania, a sposobami oceniania wielomianów opisanymi powyżej
jest natychmiastowe obniżenie oceny do zera, jeśli wielomian we
wpisanym rozwiązaniu ma za duży stopień.
Podajemy tutaj tylko odpowiednie wzory użyte
przy ocenianiu. Jeśli chcesz znaleźć dokładny opis i przykłady
oceniania, zajrzyj do dwóch pierwszych opisów oceniania wielomianów: Ocenianie
wielomianów I
i Ocenianie
wielomianów
II.
Najpierw program oblicza
parametr:
stmax
= (większy ze stopni: stopień wielomianu w prawidłowym rozwiązaniu i
stopień wielomianu w Twoim rozwiązaniu) + 1.
Następnie program liczy, ile ze współczynników
wielomianu, które wpisałeś w
rozwiązaniu jest nieprawidłowych:
w = liczba nieprawidłowych
współczynników w rozwiązaniu.
Przy ocenianiu program bierze pod uwagę następujące błędy:
Uwaga!
Wszystkie poniższe parametry przyjmują wartość 1 — gdy
opisany błąd występuje w rozwiązaniu lub 0 — gdy nie
popełniłeś danego błędu wpisując wielomian.
-
r — wielomian niezredukowany,
-
u — wielomian nieuporządkowany,
-
b — drobny
błąd.
Ostateczna ocena będzie równa:
100% – 100%
· 2
· w : stmax –
5% · (r + u) –
2% · b.
Sposoby oceniania podzbiorów liczb
rzeczywistych
Jeśli rozwiązanie zadania polega na wypisaniu
podzbiorów prostej, program ocenia rozwiązanie
biorąc pod uwagę:
-
Wnętrza
wypisanych przedziałów.
Na przykład:
Przedziały [0; 4], [0; 4), (0; 4] oraz (0;
4) mają takie samo wnętrze.
Jeśli
prawidłowe rozwiązanie ma postać [–1; 2),
a wypiszesz przedział (–1; 2),
to program zaliczy to rozwiązanie jako częściowo poprawne, gdyż wnętrza tych
przedziałów są takie same.
-
Końce przedziałów.
Na przykład:
W powyższym przykładzie, gdzie [–1; 2)
jest poprawnym rozwiązaniem, a (–1; 2)
Twoim rozwiązaniem, przedział wpisany przez ciebie
ma jeden zły koniec.
-
Zbiory
jednopunktowe.
-
Błędne
obiekty.
Na
przykład:
Jeśli prawidłowe rozwiązanie to przedział [–1; 2),
a wpiszesz [–2; 2),
to przedział [–2; 2)
uznany zostanie za błędny obiekt.
Aby obliczyć ocenę, program zlicza liczbę powyższych
obiektów. Oznaczamy:
-
w
— liczba przedziałów o prawidłowych wnętrzach, które wpisałeś,
-
k —
liczba błędnych końców
przedziałów, które wpisałeś. Uwaga!
Program zlicza błędne końce tylko tych przedziałów,
które mają prawidłowe wnętrza!
Na przykład:
Jeśli prawidłowe rozwiązanie to przedziały [–1; 2)
i (3;
6),
a wpiszesz (–1;
2)
i [3;
7),
to program odejmie punkty za jeden zły koniec, tj. koniec w
punkcie
–1.
-
j — liczba
prawidłowych zbiorów
jednopunktowych, które wpisałeś,
-
b — liczba błędnych obiektów,
które wpisałeś w rozwiązaniu.
Rozwiązanie
oceniane jest w
następujący sposób: Najpierw liczone są punkty, które uzyskałeś:
u
= 6 · w + 4 · j – 2 ·k
– 4
· b.
Następnie te punkty dzielone są przez:
r
= 6 · (liczba przedziałów w prawidłowym
rozwiązaniu) + 4 · (liczba zbiorów
jednopunktowych w prawidłowym rozwiązaniu).
Ostateczna ocena (w procentach), to:
100%
· u : r.
Przykład
rozwiązania:
Prawidłowe rozwiązanie zadania to [–4; 1].
Wpisałeś (–4; 1].
Parametry oceny: w = 1, k = 1, j = 0,
b = 0. Zatem u = 6 · 1 – 2 · 1
= 4 oraz
r = 6 · 1 = 6.
Uzyskasz 100% · 4 : 6
= 67%
punktów.
Przykład
rozwiązania:
Prawidłowe rozwiązanie zadania to {–3;
0}. Wpisałeś {–3} ∪
(–2; 0].
Parametry oceny: w = 0, k = 0, j = 1,
b = 1. Zatem u = 4 · 1 – 4 · 1
= 0 oraz r = 4 · 2 = 8.
Uzyskasz 100%
· 0 : 8 = 0
punktów.
Przykład
rozwiązania:
Prawidłowe rozwiązanie zadania to (–6; –2)
∪
(–1; 3]. Wpisałeś (–6;
–2) ∪
{–1}.
Parametry oceny: w = 1, k = 0, j = 0,
b = 1. Zatem u = 6 · 1 – 4 · 1
= 2 oraz r = 6 ·
2 = 12.
Uzyskasz 100% · 2 : 12 = 17%
punktów.
Przykład
rozwiązania:
Prawidłowe rozwiązanie zadania to [–4; 0] ∪
(1; 3] ∪ {–5; 5}. Wpisałeś (–4; 0] ∪
(1; 2] ∪ {–5; 4}.
Parametry oceny: w = 1, k = 1, j = 1,
b = 2. Zatem u = 6 · 1 + 4 · 1
– 2
· 1 – 4 · 2 = 0 oraz
r = 6
·
2 + 4 · 2 = 20.
Uzyskasz 100% · 0 : 20 = 0
punktów.
Jest to sposób oceniania podobny do opisanego
powyżej Oceniania
podzbiorów liczb rzeczywistych I. Tak jak w
metodzie powyżej, program ocenia rozwiązanie
biorąc pod uwagę:
-
Wnętrza
wypisanych przedziałów.
Na przykład:
Przedziały [0; 4], [0; 4), (0; 4] oraz (0;
4) mają takie samo wnętrze.
Jeśli
prawidłowe rozwiązanie ma postać [–1; 2),
a wypiszesz przedział (–1; 2),
to program zaliczy to rozwiązanie jako częściowo poprawne, gdyż wnętrza tych
przedziałów są takie same.
-
Końce przedziałów.
Na przykład:
W powyższym przykładzie, gdzie [–1; 2)
jest poprawnym rozwiązaniem, a (–1; 2)
Twoim rozwiązaniem, przedział wpisany przez ciebie
ma jeden zły koniec.
-
Zbiory
jednopunktowe.
-
Błędne
obiekty.
Na
przykład:
Jeśli prawidłowe rozwiązanie to przedział [–1; 2),
a wpiszesz [–2; 2),
to przedział [–2; 2)
uznany zostanie za błędny obiekt.
-
Duplikaty zbiorów skończonych.
Na
przykład:
Jeśli prawidłowe rozwiązanie to [–1;
1) ∪ {2},
a wpiszesz {2}
∪ [–1;
1) ∪ {2}, to niepotrzebne
powtórzenie zbioru {2}
zostanie uznane za błąd.
-
Liczbę zbiorów, które wypisałeś.
Na
przykład:
Jeśli prawidłowe rozwiązanie to [0; 2),
a wpiszesz [0;
1) ∪ [1,2), to zapisałeś jeden przedział jako dwa
osobne przedziały i program uzna to za błąd.
Aby obliczyć ocenę, program zlicza liczbę powyższych
obiektów. Oznaczamy:
-
w
— liczba przedziałów o prawidłowych wnętrzach, które wpisałeś,
-
k —
liczba błędnych końców
przedziałów, które wpisałeś. Uwaga!
Program zlicza błędne końce tylko tych przedziałów,
które mają prawidłowe wnętrza!
Na przykład:
Jeśli prawidłowe rozwiązanie to przedziały [–1; 2)
i (3;
6),
a wpiszesz (–1;
2)
i [3;
7),
to program odejmie punkty za jeden zły koniec, tj. koniec w
punkcie
–1.
-
j — liczba
prawidłowych zbiorów
jednopunktowych, które wpisałeś,
-
b — liczba błędnych obiektów,
które wpisałeś w rozwiązaniu.
-
d — jeśli występują duplikaty zbiorów
skończonych, to d = 1, jeśli nie, to liczba d jest równa zero,
-
z — jeśli użyłeś nieprawidłowej liczby
zbiorów, to z = 1, jeśli liczba zbiorów jest
prawidłowa, to z jest równe zero.
Rozwiązanie
oceniane jest w
następujący sposób: Najpierw liczone są punkty, które uzyskałeś:
u
= 8 · w + 8 · j – 2 ·k
– 2
· b.
Następnie te punkty dzielone są przez:
r
= 8 · (liczba przedziałów w prawidłowym
rozwiązaniu) + 8 · (liczba zbiorów
jednopunktowych w prawidłowym rozwiązaniu).
Ostateczna ocena (w procentach), to:
100%
· u : r – 20% · (d + z).
Przykład
rozwiązania:
Prawidłowe rozwiązanie zadania to [–4; 1]. Wpisałeś (–4; 1].
Parametry oceny: w = 1, k = 1, j = 0,
b = 0, d = 0, z = 0. Zatem u = 8 · 1 – 2
· 1
= 6 oraz
r = 8 · 1 = 8.
Uzyskasz 100% · 6 : 8 – 20%
· (0 + 0)
= 75%
punktów.
Przykład
rozwiązania:
Prawidłowe rozwiązanie zadania to {–3;
0}. Wpisałeś {–3} ∪
(–2; 0].
Parametry oceny: w = 0, k = 0, j = 1,
b = 1, d = 0, z = 0. Zatem u = 8 · 1 – 2
· 1
= 6 oraz r = 8 · 2 = 16.
Uzyskasz 100%
· 6 : 16 – 20% · (0 + 0) = 37%
punktów.
Przykład
rozwiązania:
Prawidłowe rozwiązanie zadania to [–4; 0] ∪
(1; 3] ∪ {–5; 5}. Wpisałeś (–4; 0] ∪
(1; 2] ∪ {–5; 4}.
Parametry oceny: w = 1, k = 1, j = 1,
b = 2, d = 0, z = 0. Zatem u = 8 · 1 + 8 · 1
– 2
· 1 – 2 · 2 = 10 oraz
r = 8
·
2 + 8 · 2 = 32.
Uzyskasz 100% · 10 : 32 –
20% · (0 + 0) = 31%
punktów.
Przykład
rozwiązania:
Prawidłowe rozwiązanie zadania to [–2;
1] ∪ {5}. Wpisałeś [–2; 0] ∪
(0; 1] ∪ {4}. Wówczas program przekształca
Twoje rozwiązanie do postaci [–2;
1] ∪ {4} i zlicza parametry oceny.
Parametry oceny: w = 1, k = 0, j = 0,
b = 1, d = 0, z = 1. Zatem u = 8 · 1 – 2
· 1 = 6 oraz
r = 8
· 1 + 8 · 1 = 16.
Uzyskasz 100% · 6 : 16 –
20% · (0 + 1) = 37% – 20% = 17% punktów.
Przykład
rozwiązania:
Prawidłowe rozwiązanie zadania to (1;
3) ∪ {–1; 5}. Wpisałeś {–1} ∪
(1; 2] ∪ (2; 3) ∪ {–1; 5}.
Wówczas program przekształca Twoje rozwiązanie do postaci (1;
3) ∪ {–1; 5} i zlicza
parametry oceny.
Parametry oceny: w = 1, k = 0, j = 1,
b = 0, d = 1, z = 1. Zatem u = 8 · 1 + 8 · 1 = 16 oraz
r = 8
· 1 + 8 · 1 = 16.
Uzyskasz 100% · 16 : 16 –
20% · (1 + 1) = 100%
– 40% = 60% punktów.
Jest to sposób oceniania analogiczny do opisanego
wcześniej Oceniania
podzbiorów liczb rzeczywistych II. Znaczenie wszystkich
parametrów opisane jest powyżej.
Ocenianie tą metodą, w odróżnieniu od Oceniania
podzbiorów liczb rzeczywistych II, cechuje się trochę
mniejszą stratą za złe końce przedziałów.
Rozwiązanie
oceniane jest w
następujący sposób: Najpierw liczone są punkty, które uzyskałeś:
u
= 8 · w + 8 · j – k
– 2
· b.
Następnie te punkty dzielone są przez:
r
= 8 · (liczba przedziałów w prawidłowym
rozwiązaniu) + 8 · (liczba zbiorów
jednopunktowych w prawidłowym rozwiązaniu).
Ostateczna ocena (w procentach), to:
100%
· u : r – 20% · (d + z).
Jest to sposób oceniania analogiczny do opisanego
wcześniej Oceniania
podzbiorów liczb rzeczywistych I. Znaczenie
wszystkich
parametrów opisane jest powyżej.
Ocenianie tą metodą, w odróżnieniu od Oceniania
podzbiorów liczb rzeczywistych I, uwzględnia
dodatkowo parametry d oraz z.
Rozwiązanie
oceniane jest w
następujący sposób: Najpierw liczone są punkty, które uzyskałeś:
u
= 6 · w + 4 · j – 2
· k
– 4
· b.
Następnie te punkty dzielone są przez:
r
= 6 · (liczba przedziałów w prawidłowym
rozwiązaniu) + 4 · (liczba zbiorów
jednopunktowych w prawidłowym rozwiązaniu).
Ostateczna ocena (w procentach), to:
100%
· u : r – 20% · (d + z).

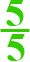 .
.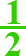 ,
a wprowadziłeś liczbę
,
a wprowadziłeś liczbę 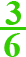 .
. zamiast
zamiast  , np. poprawne
rozwiązanie to ułamek
, np. poprawne
rozwiązanie to ułamek 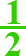 ,
a wprowadziłeś liczbę mieszaną 0
,
a wprowadziłeś liczbę mieszaną 0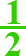 .
. oraz
oraz  oraz
oraz




